Embark on an intellectual odyssey with the axiomatic system of geometry activity 3, a meticulously crafted exploration into the fundamental principles that govern the world of shapes and spaces. This comprehensive guide delves into the historical roots, key concepts, and practical applications of this foundational system, offering a profound understanding of the language of geometry.
Through engaging explanations and illustrative examples, this discourse unveils the intricate relationships between points, lines, planes, and angles, laying the groundwork for unraveling the mysteries of geometric figures. Prepare to witness the power of axioms and postulates as they define the properties that shape our spatial world.
1. Introduction to the Axiomatic System of Geometry
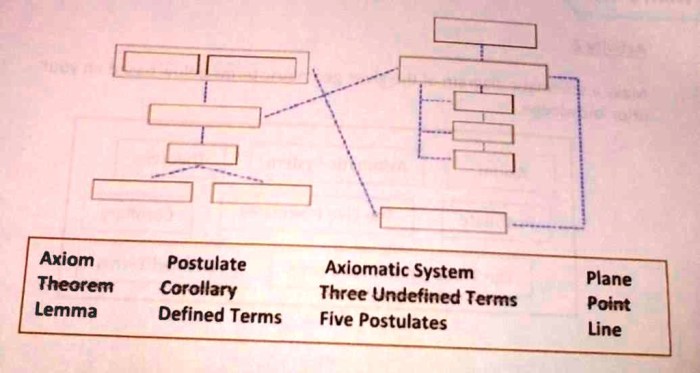
The axiomatic system of geometry is a set of rules that defines the basic properties of geometric figures. It is based on the idea that all geometric truths can be derived from a small number of axioms, which are statements that are assumed to be true without proof.
The axiomatic system of geometry was first developed by the Greek mathematician Euclid around 300 BC. Euclid’s axioms were based on the common sense observations of the world around him, and they have remained the foundation of geometry ever since.
2. Key Concepts and Definitions
The basic terms and concepts used in the axiomatic system of geometry are points, lines, planes, and angles.
- A point is a location in space that has no dimensions.
- A line is a one-dimensional object that extends infinitely in both directions.
- A plane is a two-dimensional object that extends infinitely in all directions.
- An angle is the measure of the amount of rotation between two lines.
The relationships between points, lines, planes, and angles are defined by the axioms of geometry.
3. Axioms and Postulates
The axioms of the axiomatic system of geometry are statements that are assumed to be true without proof. The postulates are statements that can be derived from the axioms.
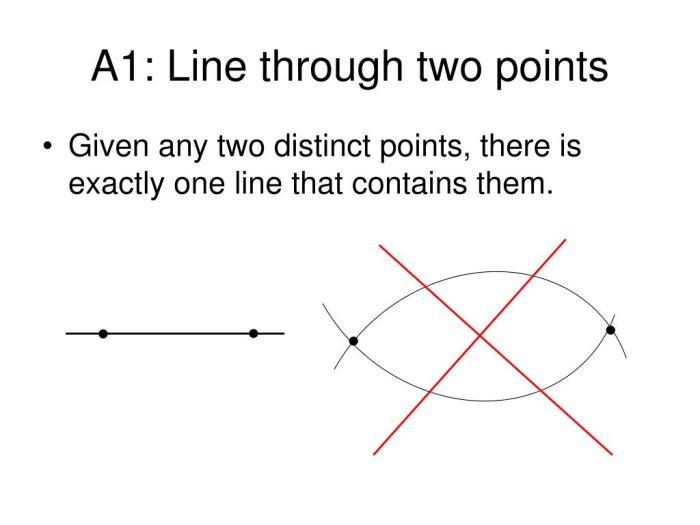
- Axiom 1:A line segment can be drawn between any two points.
- Axiom 2:A line segment can be extended indefinitely in either direction.
- Axiom 3:All right angles are congruent.
- Postulate 1:Through any point not on a given line, there is exactly one line that can be drawn parallel to the given line.
- Postulate 2:If two lines intersect, then the opposite angles are congruent.
The axioms and postulates of geometry define the basic properties of geometric figures and allow us to prove theorems about them.
4. Theorems and Proofs
A theorem is a statement that can be proven from the axioms and postulates of geometry. To prove a theorem, we must show that the statement is true for all possible cases.
One of the most famous theorems in geometry is the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
The Pythagorean theorem can be proven using the axioms and postulates of geometry. The proof is a series of logical steps that show that the theorem is true for all possible cases.
5. Applications of the Axiomatic System, The axiomatic system of geometry activity 3
The axiomatic system of geometry has many practical applications. It is used in architecture, engineering, and other fields to design and build structures.
For example, the Pythagorean theorem is used to calculate the length of the hypotenuse of a right triangle. This information can be used to design and build structures that are strong and stable.
The axiomatic system of geometry is a powerful tool that can be used to solve a wide variety of problems. It is the foundation of all of modern geometry and has applications in many different fields.
Question & Answer Hub: The Axiomatic System Of Geometry Activity 3
What is the axiomatic system of geometry?
The axiomatic system of geometry is a set of rules and assumptions that define the properties of geometric figures. It provides a foundation for proving theorems and solving geometric problems.
What are the key concepts of the axiomatic system of geometry?
The key concepts of the axiomatic system of geometry include points, lines, planes, angles, axioms, and postulates. These concepts are used to define the properties of geometric figures and to prove theorems.
What are the applications of the axiomatic system of geometry?
The axiomatic system of geometry has applications in architecture, engineering, and other fields. It is used to design buildings, bridges, and other structures, and to solve problems in navigation and surveying.